In order to hit a wide audience, I've chosen a 6th grade topic, integers. The reason for this choice is that it is one of the content areas that is often memorized, but not understood conceptually. The integers are a mathematically wonderful landscape, and opportunities to explore this landscape are usually missed. Despite the choice of using integers, the core ideas are applicable broadly.
The first step is to survey the learning landscape. I'll focus on subtracting integers, which is where things get really interesting. Typical 6th grader (skill-level) tasks with integers includes subtracting positive and negative integers.
$10-6 = 4$
$4-(-8) = 12 $
$-5 - (-8) = 3$
If I ask a middle schooler (or older student/person), why this work, the vast majority of the time I get, "I don't know. It's just how I was taught to do it." To answer why questions, one needs to understand the notion of mathematical equivalence. Equivalence is a major idea that lies at the heart of the matter, not only for integers, but also in many other areas of mathematics. Equivalence shows up in the integers via the idea that every integer can be represented in infinitely many ways using zero pairs.
$$5 = 5 + (1 - 1) = 5 + (2 - 2) = 5 + (3 - 3) = \cdots$$
Written another way,
$$5 = 6 - 1 = 7 - 2 = 8 - 3 = \cdots$$
An important developmental milestone for young students is realizing that every integer can be expressed in infinitely many different, yet equivalent ways. This idea then allows students the mathematical flexibility of choosing suitable representations to more easily enable them to solve problems and verify why things work.
\begin{eqnarray*}
-5 - (-8) &=& -5 + (8-8) - (-8) \hspace{.5in} \mbox{ (A zero pair $8-8$ is inserted) }\\
&=& [-5 + 8] + [-8 -(-8)]\\
&=& 3 + 0 \\
&=& 3
\end{eqnarray*}
Adding in a zero pair ($8-8$) allows the expression to be rearranged so that the computation can become completed using subtraction and another zero ($-8-(-8)=0$). This explanation is the bare math, so a context is useful to support the ideas for 6th graders.
Temperature is a suitable context, since negative temperature can represent degrees below the temperature water freezes (Celsius). The "Temperature Tank" model, which is based off ideas I learned from Professor John Wilkins, Cal State Dominguez Hills, allows students to model the integers using temperature and counting chips to develop their initial understanding. Contexts are important in school mathematics, because they provide a concrete base to build off of. It's not that all problems have to be real-world based. The idea is to provide a realistic enough situations to provide "handles" to the core ideas, and then let students make the generalizations and abstraction naturally.
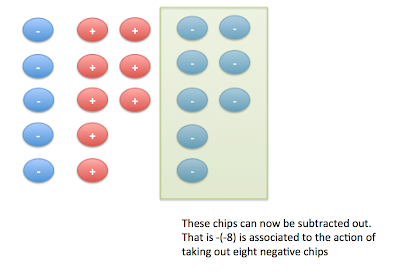
Let's see how this works for $-5-(-8)$.
A. The number $-5$ can be represented with five negative chips.
B. Using equivalence, students can choose one (of the infinitely many) representations of $-5$ that also includes an appropriate-to-the-situation zero pair. In this case, using at least 8 chips for each "partner" in the zero pair is needed.
C. Then $-8$ can be subtracted from this expression.
D. The remaining chips are used to compute the result of $-5 - (-8)$, which equals 3.
The unit starts with modeling integers with the temperature chips, and progresses to using these with operations and explaining why things work. Part of the unit is presented here.
Temperature Tank Model: A model for the integers is the temperature tank. The tank, when it has zero chips in it is at zero degrees. If you add a PLUS chip, then the temperature in the tank goes up one degree. If you add a MINUS chip, the temperature in the tank goes down one degree.
Instructions: Please model what you are doing on the open number line AND express each situation numerically.
- The tank starts off with no chips inside it and is at zero degrees. Explain what happens to the temperature of the tank, if you add three PLUS chips.
- The tank starts off with no chips inside it and is at zero degrees. Explain what happens if you add five MINUS chips.
- The tank starts off with 6 PLUS chips and 5 MINUS chips. What is the temperature of the tank?
- The tank starts off with 6 PLUS chips and 5 MINUS chips. Explain what happens to the temperature of the tank if you remove 3 PLUS chips.
- The tank starts off with 6 PLUS chips and 5 MINUS chips. Explain what happens to the temperature of the tank if you remove 3 PLUS chips, and then remove 4 MINUS chips.
- The tank starts off with 8 PLUS chips and 17 MINUS chips. Explain what happens to the tank if you take out 3 MINUS chips.
- The tank starts with 7 MINUS chips in it. Then Francisco adds 3 more MINUS chips into the tank. At what temperature is the tank?
- Definition: A zero pair is a pair of numbers that add up to zero.
- List as many zero pairs as you can, but organizing them into a table. After you create a table of all the zero pairs, explain any patterns you notice.
- How many possible different ways are there to represent using zero pairs the temperature zero degrees? Explain.
- How many different ways can you express the number 5 using the temperature tank? List at least 7 different ways.
- How many different ways can you express the number (-3) using the temperature tank? List at least 7 different ways.
- The temperature tank is at 5 degrees, and you take out of the tank 3 MINUS chips. What is the resulting temperature of the tank?
- The temperature of the tank is -3 degrees. You reach into the tank and take out 4 MINUS chips. Find what the temperature of the tank will be.
- The temperature of the tank is 10 degrees, and you take out 11 MINUS chips. What will the temperature of the tank be? Explain.
- Using the temperature tank, explain why subtracting a negative is equivalent to adding the absolute value of that number. For instance 5-(-7)=12.
- ...
Definition 8 states the zero pair, which is the core idea underlying equivalence of integers.
Problems 9-12 are intended to gently guide students to investigate the idea of equivalence. The instructor has a major role here when summarizing student discoveries. When students discover equivalence, then the instructor can jump in: "Look what you have discovered… We can now express any integer in infinitely many equivalent ways. In mathematics this is the idea of equivalence. Two expressions that are not identical represent the same number..."
Problems 13-16 hit the topic of why subtracting a negative is equivalent to adding.
The unit continues on to hit multiplication, skills, and caps with division concepts (without remainders).
Discussion
Let's break this all down. First, the task of explaining why is a much more sophisticated task compared to ones asking students to "compute the answer to…" In fact, students must put several pieces together: the context, the computation, apply concepts (zero pairs, equivalence), and express all this in writing. My belief is that this is where we want all students to go! It needs to be emphasized that picking big goals is important. It's not just about getting answers and making it through the computation. Students should own the math, and by own the math it is meant that they know how things work, how to compute, why things work the way they do, and be able to communicate their ideas clearly.
Construction of the unit has structural features that are generally present in IBL units. The beginning is usually a collection of starter problems intended to help students become familiar with a context and the basic ideas. In this case the unit starts with representing integers with a physical model.
The logical order of mathematical learning always dictates what happens next. Hence the middle phase varies. In this specific unit, an idea is needed to address the "why" questions later, thus introducing the zero pair is necessary. The middle phase is built off of developing an understanding of equivalence of integers. In general, the middle phase of a unit focuses on lemmas, key concepts, important techniques, etc. that are critical in addressing the major goals of the unit.
The last phase is encapsulated by goal problems or goal theorems. One of the big goals of the unit is for students to be able to justify why subtracting a negative is equivalent to adding. Problems 14-16 are the goal problems, and in fact were the first problems I wrote down for the unit. I start with the goal problems, and then reverse engineered what is needed logically and experientially to form the unit. This takes a bit of time and scratch work to figure out the first time, but over time it gets easier. More and more examples of problem sets (units and entire courses) are being developed by the IBL community, and the need to build materials from scratch will diminish over time.
The components of a generic IBL unit:
- Opening: units open with starter problems, definitions, assumptions, and establishing the context/topic. (Starter problems may need to be interspersed throughout the unit.)
- Middle Phase: the middle phase is the main building phase of the ideas, techniques, and mathematical perspectives. The building blocks should contain the core mathematical building blocks, which are usually found by reverse engineering.
- Goal Problems: the big learning goals of the unit are usually at the end of the unit. The goal problem phase may also include applications.
- Wrap-up: reflecting and organizing what has been learned is highly valuable, and often a good way end a unit. Additional applications for formative assessment purposes to ensure the goals have been met can also be implemented in the wrap-up.
More examples are forthcoming from different levels of mathematics. I hope this post highlights that IBL math is more than just a collection of problems, implemented so that students are required to work on the problems and present them. That captures only a fraction of the IBL framework. Units are composed with a story or narrative, and designed to support a natural arc of learning. Moreover, the units are not fixed. They can be adapted over time, and it is expected that an instructor must add or subtract problems in class to adapt to specific learning needs with each class.
Does this specific unit on integers work? Yes! The unit is not some theoretical prototype I cooked up in the lab. It was designed, implemented and updated from actual classrooms. In fact, the unit has been used multiple times in 6th grade classrooms, where students successfully make it through all of the problems, explaining how and why things work, all the while learning the skills, too. The full unit is posted HERE and HERE. You are free to use it, change it, make it better.
In comparison, a conventional, teacher-centered unit, where mathematical equivalence is not included, usually means that answering why questions is out of reach for students. A conventional framework may include diagrams/schemes (e.g. subtracting a negative is jumping to the right), which is merely a restatement of the rule using the number line. These essentially boil down to, "Here is how to calculate these things, and here are some heuristics to help memorize them." There are many limitations to such a learning arc, and one of the main limitations is not providing students the mathematical foundations for making sense of the fundamental ideas and building viable mathematical arguments to explain them. On the other hand, building upon the bedrock of mathematics, providing entry points for all students, and opportunities to explore, experiment, and explain, gives students a chance to truly own it and develop as young mathematicians.
Believe in your students!